論理式が矛盾しているかどうかを判定する

昔論理学の授業で習ったタブロー法を Scheme と SLLGEN で実装してみました。

* 速習タブロー法

タブロー法とは論理式が充足可能か矛盾しているかを確かめるアルゴリズムの一つです。

充足可能というのはその論理式が真になるような場合がありうるかということです。例えば P&Q は P が 真で Q も真であれば真になるので充足可能です。一方で P&~P は P が真であっても偽であっても真になりえないので矛盾しています。

タブロー法は

1. 与えられた論理式が全て充足可能であると仮定する
2. 論理式を展開規則によって原子式まで分解して行く。例えば「A&B=真」という仮定からは「A=真」「B=真」という2つの仮定が生じます。
3. 分解していく過程でなんらかの原子式Pについて「P=真」と「P=偽」の両方が現れたら矛盾。最後まで矛盾しなかったら充足可能。

という手順を踏んでいきます。展開規則は論理式を単純化していく方向にしか進まないので手順は必ずそのうち止まります。

また手順は分岐することもあります。例えば「A∨B=真」という仮定は「A=真」と仮定して先に進むか、「B=真」と仮定して先に進むかして、どっちかで充足可能であれば OK ということになります。

ちょっと複雑な式で例を挙げると以下の図のようになります。

演算子 &, ∨, →, ~ を使う論理式について展開規則をリストアップすると以下になります。

- A&B ⇒ AとBに分解
- A∨B ⇒ 分岐して一方にA、もう一方にB
- A→B ⇒ 分岐して一方に~A、もう一方にB
- ~(A&B) ⇒ 分岐して一方に~A、もう一方に~B
- ~(A∨B) ⇒ ~Aと~Bに分解
- ~(A→B) ⇒ Aと~Bに分解
- 原子式 P ⇒ Pは真として矛盾が無いか確かめる
- 原子式の否定 ~P ⇒ Pは偽として矛盾が無いか確かめる

* 論理式のパーサを作る

まずは論理式をプログラムで取り扱える形式にするために SLLGEN でパーサを作ります。論理式の文法というのは大体こんな感じです。

expression := <atom>
| ~ <expression>
| ( <expression> & <expression> )
| ( <expression> ∨ <expression> )
| ( <expression> → <expression> )

これをそのまま SLLGEN 用の文法定義に書けたらよいのですが、これは SLLGEN に受け入れられません。理由は SLLGEN が LL(1) の文法しか受け入れてくれないという大人の事情があるためで、これは1文字読んだだけでどの置き換え規則を使えばいいのか判断できないといけないということです。上記の規則は開き括弧に出会ったときの選択肢が3つ存在していて判断ができないため NG です。そこで文法を下記のように変えます。

expression := <atom>
| ~ <expression>
| ( <expression> <expr-rest> )
exp-rest := 
| & <expression>
| ∨ <expression>
| → <expression>

これを SLLGEN 用に書くとこうなります。

(define grammar-logic
  '((expression (identifier) atom)
    (expression ("~" expression) neg)
    (expression ("(" expression exp-rest ")") binary)
    (exp-rest ("&"  expression) partial-conj)
    (exp-rest ("|"  expression) partial-disj)
    (exp-rest ("->" expression) partial-cond)))

しかしこれによってできるデータ構造は元々ほしかったものではありません。

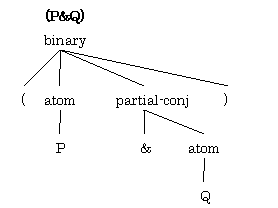
partial-conj というのが変です。これは左辺が足りなくて式になりきれていない不完全な構成素です。逆に言うと左辺が与えられれば式になれるということで、そのことを Scheme 風の言葉で表現すると (lambda (x) <<x & Q>>) ということになります。そうすると上の binary という構成素を関数適用と考えて変換すれば辻褄があうということが分かります。以上を踏まえてパーサはこうなりました。

(load "r5rs.scm")
(load "define-datatype.scm")
(load "sllgen.scm")

(define scanner-spec-logic
  '((white-sp
      (whitespace) skip)
    (identifier
      (letter) symbol)))

(define grammar-logic
  '((expression (identifier) atom)
    (expression ("~" expression) neg)
    (expression ("(" expression exp-rest ")") binary)

    (exp-rest ("&"  expression) partial-conj)
    (exp-rest ("|"  expression) partial-disj)
    (exp-rest ("->" expression) partial-cond)

    (expression ("[&"  expression expression "]") conj) ; dummy rule
    (expression ("[|"  expression expression "]") disj) ; dummy rule
    (expression ("[->" expression expression "]") cond) ; dummy rule
    ))

(sllgen:make-define-datatypes scanner-spec-logic grammar-logic)

(define make-exp
  (lambda (exp)
    (cases expression exp
      (atom (sym) exp)
      (neg (exp) (neg (make-exp exp)))
      (binary (exp rest) ((make-rest rest) (make-exp exp)))
      (else exp)
      )))

(define make-rest
  (lambda (exp)
    (cases exp-rest exp
      (partial-conj (rest) (lambda (x) (conj x (make-exp rest))))
      (partial-disj (rest) (lambda (x) (disj x (make-exp rest))))
      (partial-cond (rest) (lambda (x) (cond x (make-exp rest))))
      )))

(define parse
  (lambda (input)
    (make-exp
      ((sllgen:make-string-parser scanner-spec-logic grammar-logic) input))))

grammar-logic の最後の3つはダミールールで、これを入れておくことにより SLLGEN が自動生成してくれるデータ構造に本来欲しかった構造も付け加えることが出来ます。こうしない場合は自分で define-datatype を書けばよいです。

* タブロー法を実装する

続いて論理式が充足可能かどうか調べる satisfiable? 関数を作ります。これは先ほどのタブロー展開規則をこつこつ Scheme に直していきます。

(define satisfiable?
  (lambda (exps bindings)
    (if (null? exps)
      bindings
      (cases expression (car exps)
        (atom (sym)
          (let ((new-bindings (unify sym #t bindings)))
            (and new-bindings (satisfiable? (cdr exps) new-bindings))))
        (conj (l r)
          (satisfiable? (append (cdr exps) (list l r)) bindings))
        (disj (l r)
          (or
            (satisfiable? (append (cdr exps) (list l)) bindings)
            (satisfiable? (append (cdr exps) (list r)) bindings)))
        (cond (l r)
          (or
            (satisfiable? (append (cdr exps) (list (neg l))) bindings)
            (satisfiable? (append (cdr exps) (list r)) bindings)))
        (neg (exp)
          (cases expression exp
            (atom (sym)
              (let ((new-bindings (unify sym #f bindings)))
                (and new-bindings (satisfiable? (cdr exps) new-bindings))))
            (conj (l r)
              (or
                (satisfiable? (append (cdr exps) (list (neg l))) bindings)
                (satisfiable? (append (cdr exps) (list (neg r))) bindings)))
            (disj (l r)
              (satisfiable? (append (cdr exps) (list (neg l) (neg r))) bindings))
            (cond (l r)
              (satisfiable? (append (cdr exps) (list l (neg r))) bindings))
            (neg (exp)
              (satisfiable? (append (cdr exps) (list exp)) bindings))
            (else (eopl:error 'satisfiable? ""))
            ))
        (else (eopl:error 'satisfiable? ""))
        ))))

(define unify
  (lambda (sym val bindings)
    (let ((v (assoc sym bindings)))
      (if v
        (if (eqv? val (cdr v))
          bindings
          #f)
        (cons (cons sym val) bindings)))))

satisfiable? の第1引数 exps は真と仮定される論理式のリストで最初は与えられた論理式が入りますが、展開をしていくにつれて増えたり減ったりします。展開はこのリストから1つ取って展開規則にしたがって分解したものをお尻にくっつけるという形で進行します（頭にくっつけてもいいと思う）。bindings 引数は上のタブロー図でいうと吹き出しの中に相当する部分で、これまでの展開でどの原子式が真ないし偽とされているかを保持します。

原子式の真偽が確定した時点で呼び出されるのが unify 関数で、これはもし原子式がまだ吹き出しの中に無かったら新たに原子式とその値を追加します。既にあった場合は既存の値と新しい値が矛盾するかどうかをチェックし、一致した場合はそのまま、不一致であれば #f を返します。

最後にテストをしてみます。

gosh> (satisfiable? (list (parse "(P&((Q&~P)|~P))")) '())
#f
gosh> (satisfiable? (list (parse "((~P|Q)->(P->Q))")) '())
((P . #t) (Q . #f))
gosh> (satisfiable? (list (parse "((P&Q)->~~P)")) '())
((P . #f))
gosh> (satisfiable? (list (parse "(P&~P)")) '())
#f

以上タブロー法でした。