Ruby による LFG

Bresnan の書いた LFG (Lexical Functional Grammar) の入門テキスト "Lexical Functional Syntax" の最初の方を読んだ。これが面白かったので Ruby による実装に挑戦してみた。

* 速習 LFG

LFG は Chomsky 流の生成文法とは違ってひとつの文についてひとつの統語表示だけを与える。その代わりに統語表示以外にもいくつかの構造を利用していて、マッピングルールによってそれらを結びつける（「変形」や「移動」ではない）という考え方をとっている。
最も基本となる構造は c-structure と f-structure で、前者はいわゆる統語構造（c は constituent）で後者は主語や目的語といった文法概念が登場する素性構造（f は feature または function）である。

見るが早しということで例を挙げると "Lions sleep." という文には以下のような c-structure と f-structure が与えられる。

c-structure:

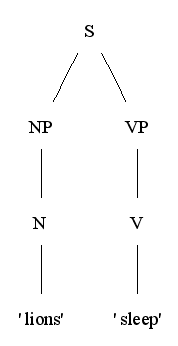
f-structure:

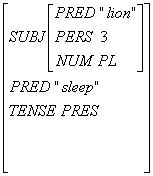
c-structure はツリー構造、f-structure はプログラミング言語でいうところの連想配列の構造を持つが、階層的になっていてもよい。

c-structure から f-structure へのマッピングルールは文脈自由法の個々の置き換え規則および単語の辞書内に以下のように記載された等式群を利用する（この文法はもちろん部分的なもの）。

「↑ = ↓」は大体「上位ノードに対応付けられる f-structure とこのノードに対応づけられる f-structure が同じ」と読む。「(↑ SUBJ) = ↓」は「上位ノードに対応付けられる f-structure の SUBJ 素性の値がこのノードに対応づけられる f-structure である」。そして「(↑ NUM) = PL」は「上位ノードに対応付けられる f-structure の NUM 素性の値が PL である」、などなど。

"Lions sleep." の c-structure のノードにそれぞれ対応付けられる f-structure の名前を付与してみよう。

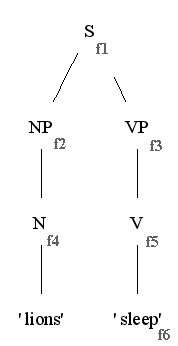
これにしたがって先ほどの等式群を置き換えると以下のような等式群が得られる。

(f1 SUBJ) = f2
f1 = f3
f2 = f4
f3 = f5
(f4 PRED) = 'lion'
(f4 NUM) = PL
(f5 PRED) = 'sleep'
(f5 TENSE) = PRES
(f5 SUBJ) = f6
(f6 PERS) = 3
(f6 NUM) = PL

この等式を順番に解決していくと以下のようになる。

(f1 SUBJ) = f2

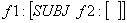
f1 = f3

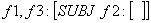
f2 = f4

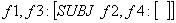
f3 = f5

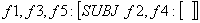
(f4 PRED) = 'lion'

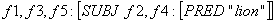
(f4 NUM) = PL

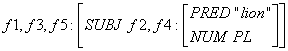
(f5 PRED) = 'sleep'

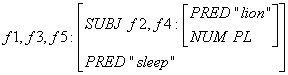
(f5 TENSE) = PRES

(f5 SUBJ) = f6

(f6 PERS) = 3 および (f6 NUM) = PL

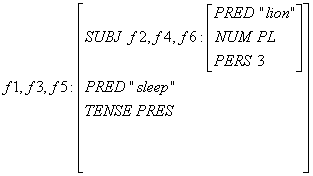
結果として目的の f-structure が出来上がっていることがわかる。

最後の (f6 NUM) = PL を解決するところで f2=f4=f6 の NUM にはすでに PL が埋まっていることに注目されたい。この場所に同じ PL がくるためにこれらの等式は矛盾なく成立するということになる。

これが "*Lions sleeps." のような非文の場合、sleeps の辞書には (↑ NUM) = PL の代わりに (↑ NUM) = SG が登録されている。そうすると最後の部分ですでに作られている構造と矛盾することになってこの文は成立しない。LFG ではこのようにしていわゆる数の一致が説明できる。

* 実装

インターネットで検索すると LFG の実装がいくつかみつかるが、どれも Prolog を使っているようだ。私は Prolog はさっぱり（いつか習得したいけど）なので代わりに Ruby を用いたい。Ruby だとハッシュが使えるので素性構造の表現もしやすそうだ（今回はオブジェクト指向はほとんど使わない）。

等式の解決はいわゆる単一化と呼ばれるもので、Reasoned Schemer の "Under the hood" の章の Scheme 実装を参考にした。

** 環境

f1 = f3 と f3 = f5 がすでに与えられているときに、「f1 の値は？」と「f3 の値は？」と「f5 の値は？」という質問には同じ答えを与えなければならない。このように何と何が同じという知識を蓄えるデータベースが必要だ。このデータベース（環境）は変数から値へのハッシュとして表現できる。変数の値がさらに別の変数だったらもう1回その別の変数の値を探すことによって上記の要件を満たすことができる。

class Var; end

# 環境sを元に変数vの値を返す。vが未束縛の場合はvを返す。
def walk(v, s)
  if v.kind_of?(Var) then
    a = s[v]
    if a then
      return walk(a, s)
    else
      return v
    end
  else
    return v
  end
end

Var は変数をあらわすクラスで、これは「変数である」という判定ができるオブジェクトであればなんでもよいので定義は空である。Ruby では kind_of? メソッドでクラスの判定ができる。walk メソッドは環境 s に基づいて与えられた変数の値を返すが、値が変数だった場合はその変数をもとに再帰的に値を検索していく。結局未定義だった場合は変数そのままで返す。

**単一化

等式がひとつひとつ与えられる段階ではこの環境をどんどん拡張していくことになる。まずは単純にハッシュを拡張するためのメソッド。

# x→vでsを拡張して返す（非破壊的）
def ext_s(x, v, s)
    new_s = s.clone
    new_s[x] = v
    return new_s
end

これを使って単一化をするためのメソッドは以下。

# 環境sにおいてvとwを単一化して新しい環境sを返す
# 単一化できなければnil
def unify_s(v, w, s)
  return nil unless s
  v = walk(v, s)
  w = walk(w, s)
  case
  when v.equal?(w) then return s
  when v.kind_of?(Var) then return ext_s(v, w, s)
  when w.kind_of?(Var) then return ext_s(w, v, s)
  when v.kind_of?(Hash) && w.kind_of?(Hash) then
    v.each{|key, value| if w[key] == nil then w[key] = value end}
    w.each{|key, value| if v[key] == nil then v[key] = value end}
    return v.inject(s){|new_s, pair| unify_s(pair[1], w[pair[0]], new_s)}
  when v == w then return s
  end
end

v と w は最初に walk にかけて正規化する。その上で v = w であればそのままの環境、どちらかが変数であれば新しいバインディングを追加した環境を返す。このへんは Reasoned Schemer そのまま。

付け加えたのは共にハッシュだった場合の処理で、この場合はお互いに足りないキーの値を埋めてあげた後で個々の値を単一化している。これは {:NUM=>:PL} と {:NUM=>:SG} は矛盾しないといけないが、{:PRED=>'lion'} と {:NUM=>:PL} は単一化に成功する必要があるためだ。（この辺の処理が破壊的操作になっているのがいまいちな気もするけど他にやりようがあるのかよくわからない）

(f1 SUBJ) = f2 のような形式の単一化のためのメソッドも作った。

def lookup_o(h, k, v, s)
  return nil unless s
  h = walk(h, s)
  v = walk(v, s)
  case h
  when Var then
    ext_s(h, {k=>v}, s)
  when Hash then
    if h[k] != nil then
      return unify_s(h[k], v, s)
    else
      # destructive
      h[k] = v
      return s
    end
  else
    return
  end
end

** 文法と辞書

残すは文法と辞書。c-structure は以下のような形式で与えられるものとする。

c_structure = [:S, [:NP, [:N, "lions"]], [:VP, [:V, "sleep"]]]

文法と辞書に対応するものがこれ。

class Array
  def rest
    return self[1..-1]
  end
end

def match(s, lhs, rhs)
  case rhs
  when Array then
    return s[0] == lhs && s.rest.map{|x| x[0]} == rhs
  else
    return s[0] == lhs && s[1] == rhs
  end
end

def c2f(c, s, up)
  case
  when match(c, :S, [:NP, :VP]) then
    np = Var.new
    vp = Var.new
    s = lookup_o(up, :SUBJ, np, s)
    s = unify_s(up, vp, s)
    s = c2f(c[1], s, np)
    s = c2f(c[2], s, vp)
    return s
  when match(c, :NP, [:N]) then
    down = Var.new
    s = unify_s(up, down, s)
    s = c2f(c[1], s, down)
    return s
  when match(c, :VP, [:V]) then
    down = Var.new
    s = unify_s(up, down, s)
    s = c2f(c[1], s, down)
    return s
  when match(c, :N, "lions") then
    s = lookup_o(up, :PRED, "lion", s)
    s = lookup_o(up, :NUM, :PL, s)
    return s
  when match(c, :V, "sleep") then
    s = lookup_o(up, :PRED, "live", s)
    s = lookup_o(up, :TENSE, :PRES, s)
    down = Var.new
    s = lookup_o(up, :SUBJ, down, s)
    s = lookup_o(down, :NUM, :PL, s)
    s = lookup_o(down, :PERS, 3, s)
    return s
  when match(c, :V, "sleeps") then
    s = lookup_o(up, :PRED, "live", s)
    s = lookup_o(up, :TENSE, :PRES, s)
    down = Var.new
    s = lookup_o(up, :SUBJ, down, s)
    s = lookup_o(down, :NUM, :SG, s)
    s = lookup_o(down, :PERS, 3, s)
    return s
  end
end

ここは我ながら汚すぎてどうかと思うけど、本当ならもうちょっとデータ駆動な感じであるべきところ。

** 実行と pretty printing

この c2f メソッドを使って以下のようにするとすべての等式が解決された環境が得られる。

top_f = Var.new
s = c2f(c_structure, {}, top_f)

なお、ここで p s[top_f] とか p walk(top_f, s) とやっても以下のような表示になってしまう。

{:TENSE=>:PRES, :SUBJ=>#<Var:0x293b0c8>, :PRED=>"live"}

つまりハッシュの中に Var クラスのオブジェクトが出てくる場合はそれも環境に照らして walk したものを表示してあげる必要がある。

def walk_star(v, s)
  v = walk(v, s)
  case v
  when Var then return v
  when Hash then
    return v.inject({}){|hsh, pair|
      hsh[pair[0]] = walk_star(pair[1], s)
      hsh
    }
  else return v
  end
end

p walk_star(top_f, s) if s

この walk_star メソッドをつかうと無事以下のような結果が得られる。

{:TENSE=>:PRES, :SUBJ=>{:NUM=>:PL, :PERS=>3, :PRED=>"lion"}, :PRED=>"live"}

一方で "Lions sleeps." を与えると s は nil になり、単一化は失敗する。

c_structure = [:S, [:NP, [:N, "lions"]], [:VP, [:V, "sleeps"]]]
top_f = Var.new
s = c2f(c_structure, {}, top_f)
p walk_star(top_f, s) if s

2007-04-10追記:

上記のプログラムにはバグがあった。問題は Hash を単一化する部分で、これは以下のような例でうまくいかない。

f1 = Var.new
f2 = Var.new
f3 = Var.new
s = {}
s = lookup_o(f1, :A, 1, s)
s = lookup_o(f2, :B, 2, s)
s = lookup_o(f3, :C, 3, s)
p s
s = unify_s(f1, f2, s)
s = unify_s(f1, f3, s)
p s
p walk(f1, s)
p walk(f2, s)
p walk(f3, s)

この例だと f1=f2=f3 なので最後の3つはどれも {:A=>1, :B=>2, :C=>3} になってほしいところだが実際には f2 だけ {:A=>1, :B=>2} となる。f1 と f2 の単一化で両者のハッシュを互いに埋め合わせたのはいいが、実体としては別オブジェクトのままなので f1 と f3 の単一化で f2 だけおいてけぼりになるのだ。これを直したつもりの unify_s は以下である。

def unify_s(v, w, s)
  return nil unless s
  v = walk(v, s)
  w = walk(w, s)
  case
  when v.equal?(w) then return s
  when v.kind_of?(Var) then return ext_s(v, w, s)
  when w.kind_of?(Var) then return ext_s(w, v, s)
  when v.kind_of?(Hash) && w.kind_of?(Hash) then
    s = s.clone
    new_h = v.merge(w) {|k, lhs, rhs|
      s = unify_s(lhs, rhs, s)
      lhs
    }
    return s.each{|key, val|
      if val.equal?(v) or val.equal?(w) then s[key] = new_h end
    }
  when v == w then return s
  end
end